ROBOT
Return of Bleichenbacher's Oracle Threat
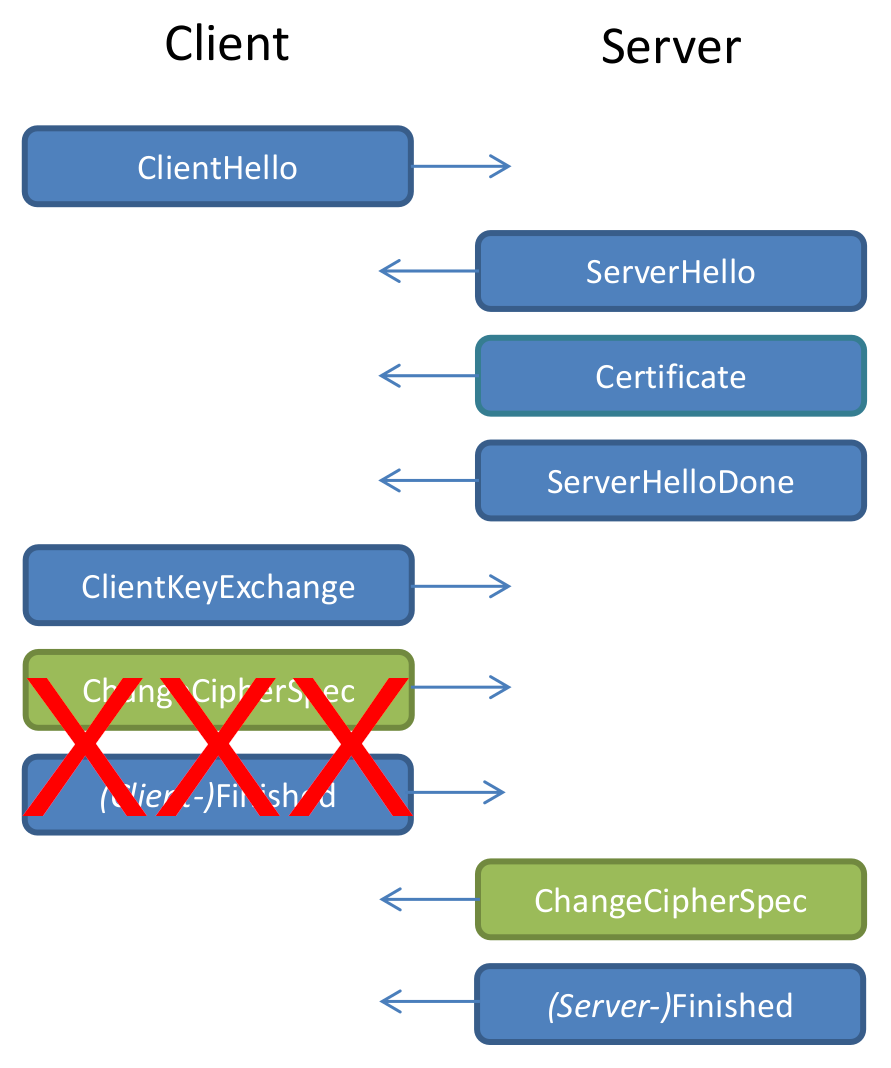
Let's look at the TLS handshake
Client and Server want to get a Shared Secret
Two ways
- RSA Encryption
- Diffie Hellman (DHE or ECDHE) with Signatures (usually RSA), provides forward secrecy
Let's look at RSA Encryption
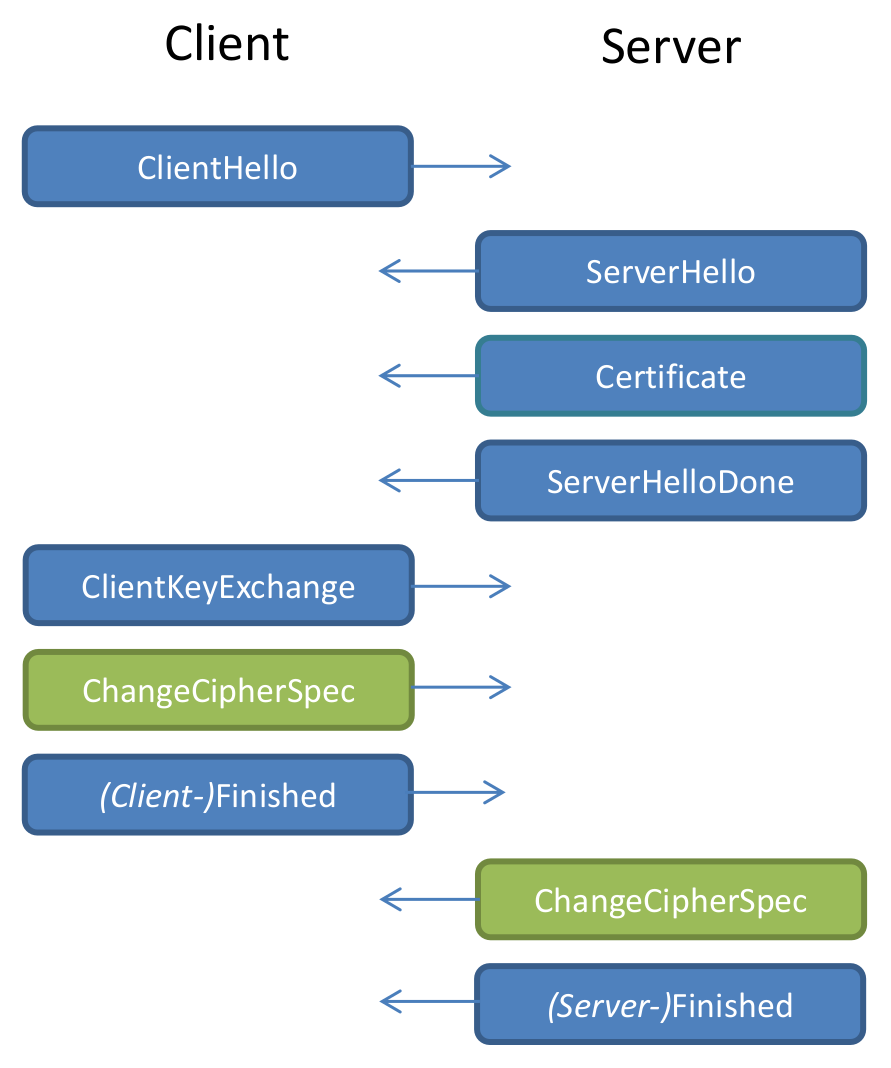
ClientKeyExchange
RSA-Encrypted Pre-Master Secret (random data)Naive RSA encryption
Message M · public key e, N · private key d
Encrypt: E = Me mod N
Decrypt: M = Ed mod N
This naive variant is called Textbook RSA and totally insecure.
Why?
Encrypting the messages "0" and "1":
E = 0d mod N = 0
E = 1d mod N = 1
Padding
PKCS #1 1.5
Padding in TLS RSA Encryption
00 | 02 | [random] | 00 | 03 | 03 | [secret]
00 | 02 | [random] | 00 | 03 | 03 | [secret] ^^^^^^^
Block type (encryption)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes without zeros
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^
End of padding
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^
TLS Version from ClientHello
03 03 stands for TLS 1.2
(Don't ask, other story...)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes

Decrypted RSA block must always start with 00 02.
What should the server do if it doesn't?
Idea: Just reject the message with an error.
(e. g. "wrong block type prefix")
We just gave an attacker some information about encrypted data.
Correct prefix:
00 02 00 [...] 00 <= M < 00 03 00 [...] 00
Bad prefix:
M < 00 02 00 [...] 00 or M >= 00 03 00 [...] 00
RSA Malleability
2e * RSAEnc(M) = RSAEnc(2*M) 3e * RSAEnc(M) = RSAEnc(3*M) ne * RSAEnc(M) = RSAEnc(n*M)
RSA operates on numbers
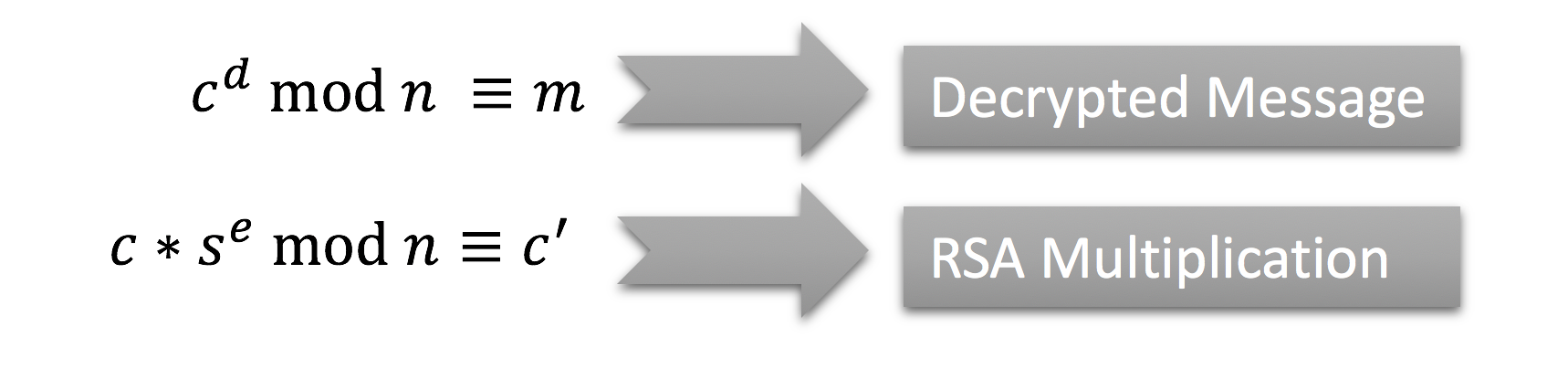
Valid padding implies m*s starts with 0x0002
So what?
Let's consider a basic example...


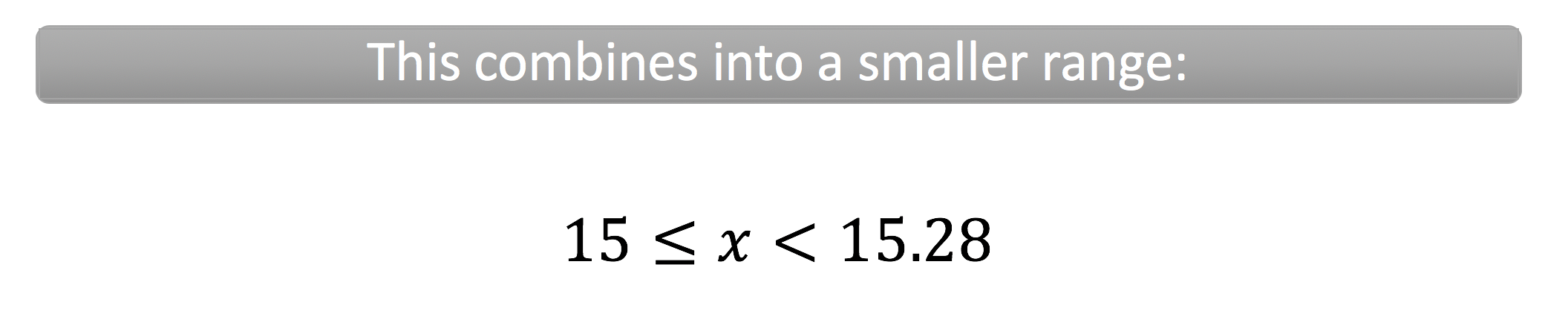
Each "conforming" value narrows the range
This works for RSA too...
...but it's a little more complicated
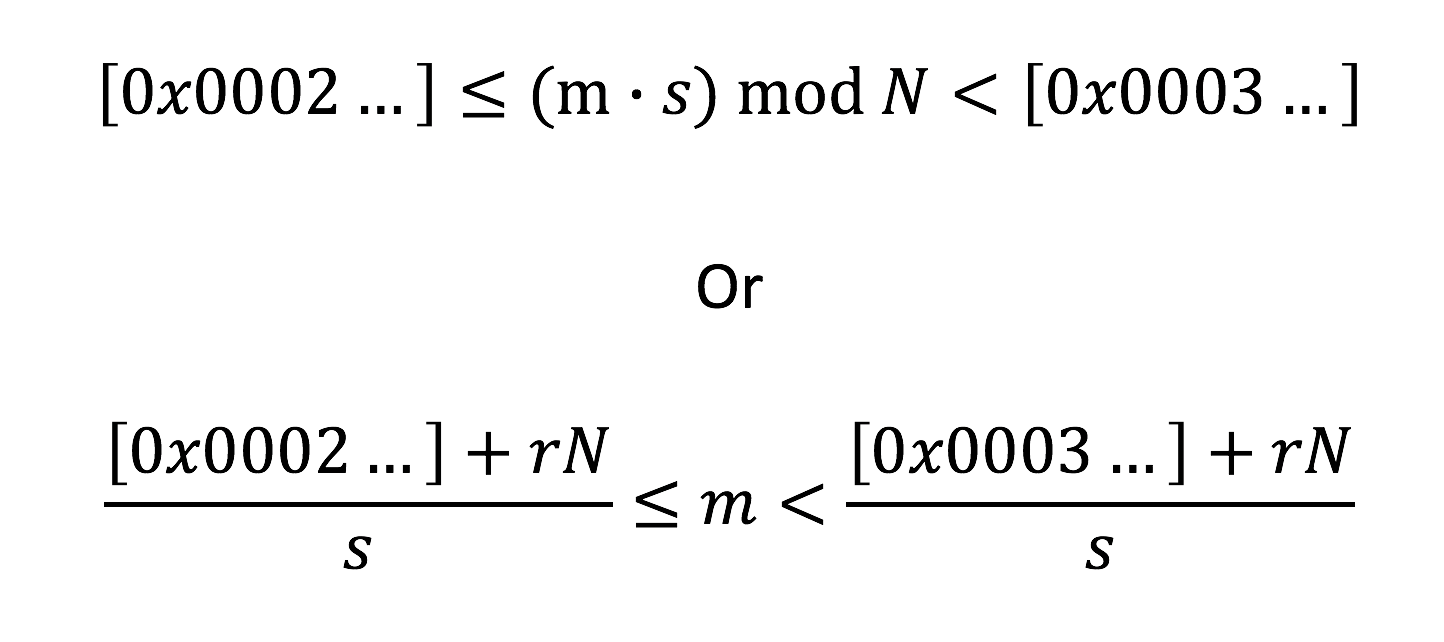
TL;DR is that each positive response from the oracle narrows in on the decrypted value
After enough oracle queries, the range is small enough to brute force search
Variations
00 | 02 | [random] | 00 | 03 | 03 | [secret]
Depending on the checks done by the server (block prefix, padding length, TLS version) we get different oracles.
The "strength" of an oracle depends on which checks are revealed by the server.
How to fix?
Server must not give the client any information about the decrypted data.
The best way to avoid vulnerability to this attack is to treat incorrectly formatted messages in a manner indistinguishable from correctly formatted RSA blocks. Thus, when it receives an incorrectly formatted RSA block, a server should generate a random 48-byte value and proceed using it as the premaster secret. Thus, the server will act identically whether the received RSA block is correctly encoded or not.
In case of a bad padding a server should pretend everything is alright and replace the decrypted data with a random value.
As described by Klima [KPR03], these vulnerabilities can be avoided
by treating incorrectly formatted message blocks and/or mismatched
version numbers in a manner indistinguishable from correctly
formatted RSA blocks. In other words:
1. Generate a string R of 46 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = ClientHello.client_version || R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
pre_master_secret = M
else:
pre_master_secret = ClientHello.client_version || M[2..47]
Note that explicitly constructing the pre_master_secret with the
ClientHello.client_version produces an invalid master_secret if the
client has sent the wrong version in the original pre_master_secret.
An alternative approach is to treat a version number mismatch as a
PKCS-1 formatting error and randomize the premaster secret
completely:
1. Generate a string R of 48 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
premaster secret = M
else If M[0..1] != ClientHello.client_version:
premaster secret = R
else:
premaster secret = M
Although no practical attacks against this construction are known,
Klima et al. [KPR03] describe some theoretical attacks, and therefore
the first construction described is RECOMMENDED.
In any case, a TLS server MUST NOT generate an alert if processing an RSA-encrypted premaster secret message fails, or the version number is not as expected. Instead, it MUST continue the handshake with a randomly generated premaster secret. It may be useful to log the real cause of failure for troubleshooting purposes; however, care must be taken to avoid leaking the information to an attacker (through, e.g., timing, log files, or other channels.)
A server generates a random value before parsing the message, just in case.
If the message has a bad padding then the server is supposed to replace it with the random value.
If the message has a bad version then the server can choose whether to replace it with a random value or to fix the version.
The second variant is better, but we like to make the standard longer, therefore we describe both and let the implementor choose.
By the way: Everything must be timing-safe. Please figure out how to do that.
Totally easy!
Of course everyone will get this right.
This attack has been known since 1998 and is well documented, so everyone has a regression test for it, right?
Maybe not...
Let's test
Send different broken RSA-encrypted ClientKeyExchange packages.
If replies differ we have an oracle.
TLS alerts, Duplicate TLS alerts, TCP connection resets, Timeouts
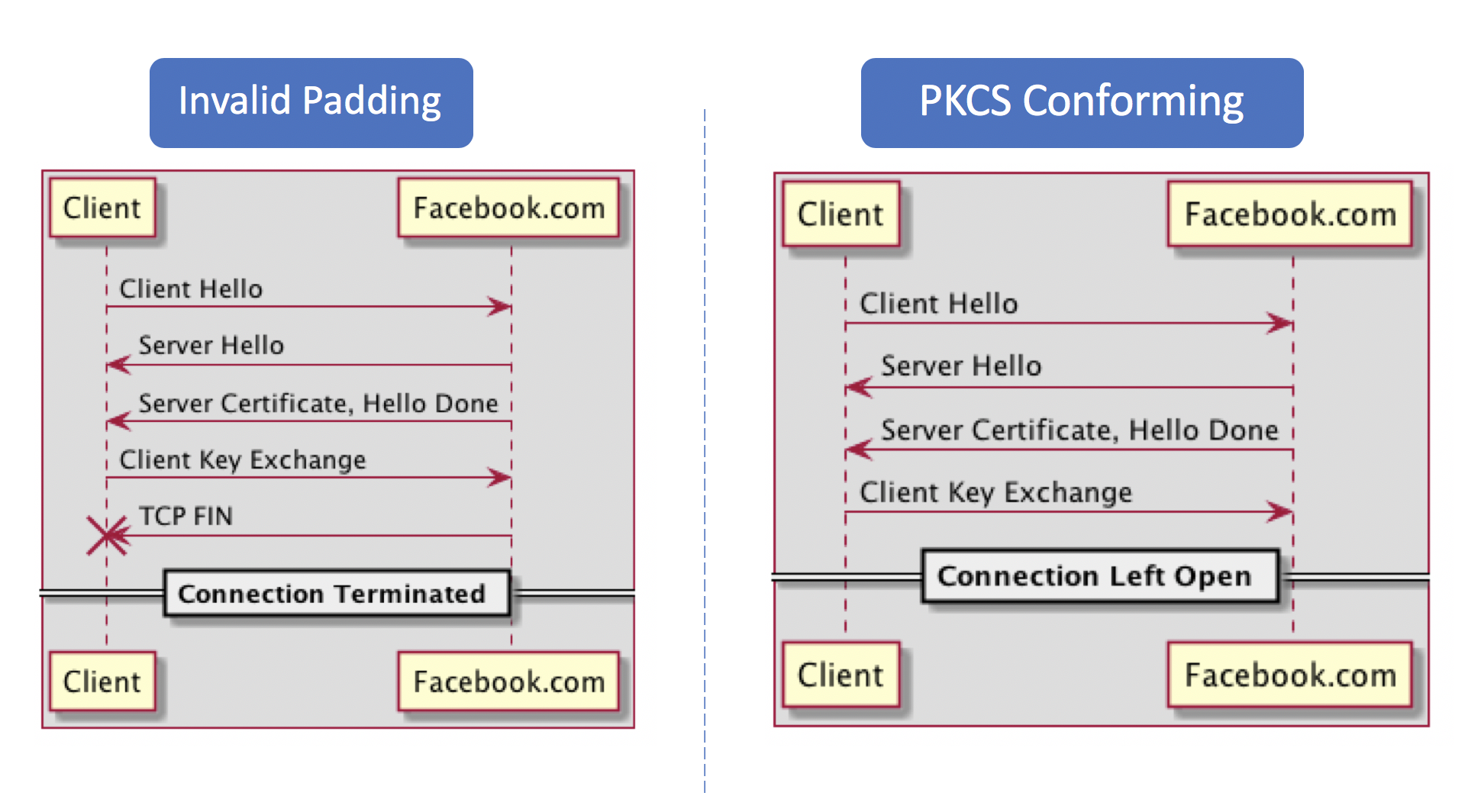
First hit: facebook.com
We have to attack Facebook!
Goal: We would like to sign a message with the private key from facebook.com.
This attack needs tens of thousands of connections, so we want to be fast.
We tried all AWS locations, on some we got ping times to facebook around 2-3 ms.
Eventually we figured out that our attack ran much faster with TCP_NODELAY set.
After several tries we did it! We successfully signed a message with Facebook's private key.
We reported it to Facebook. They fixed it.
Facebook.com now sends a generic TLS alert...

But what happens if we alter the message flow?
Facebook's Shortflow Oracle
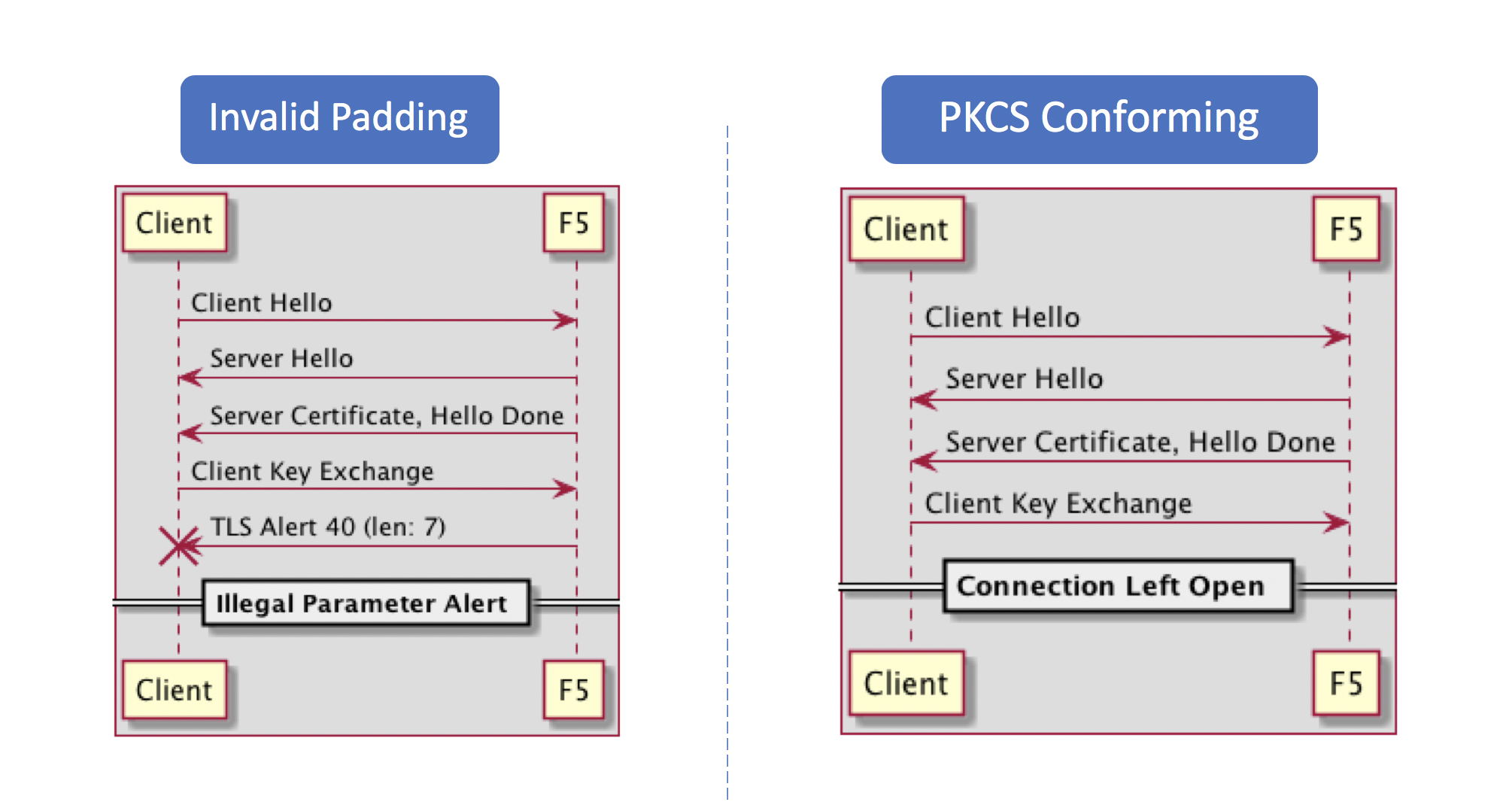
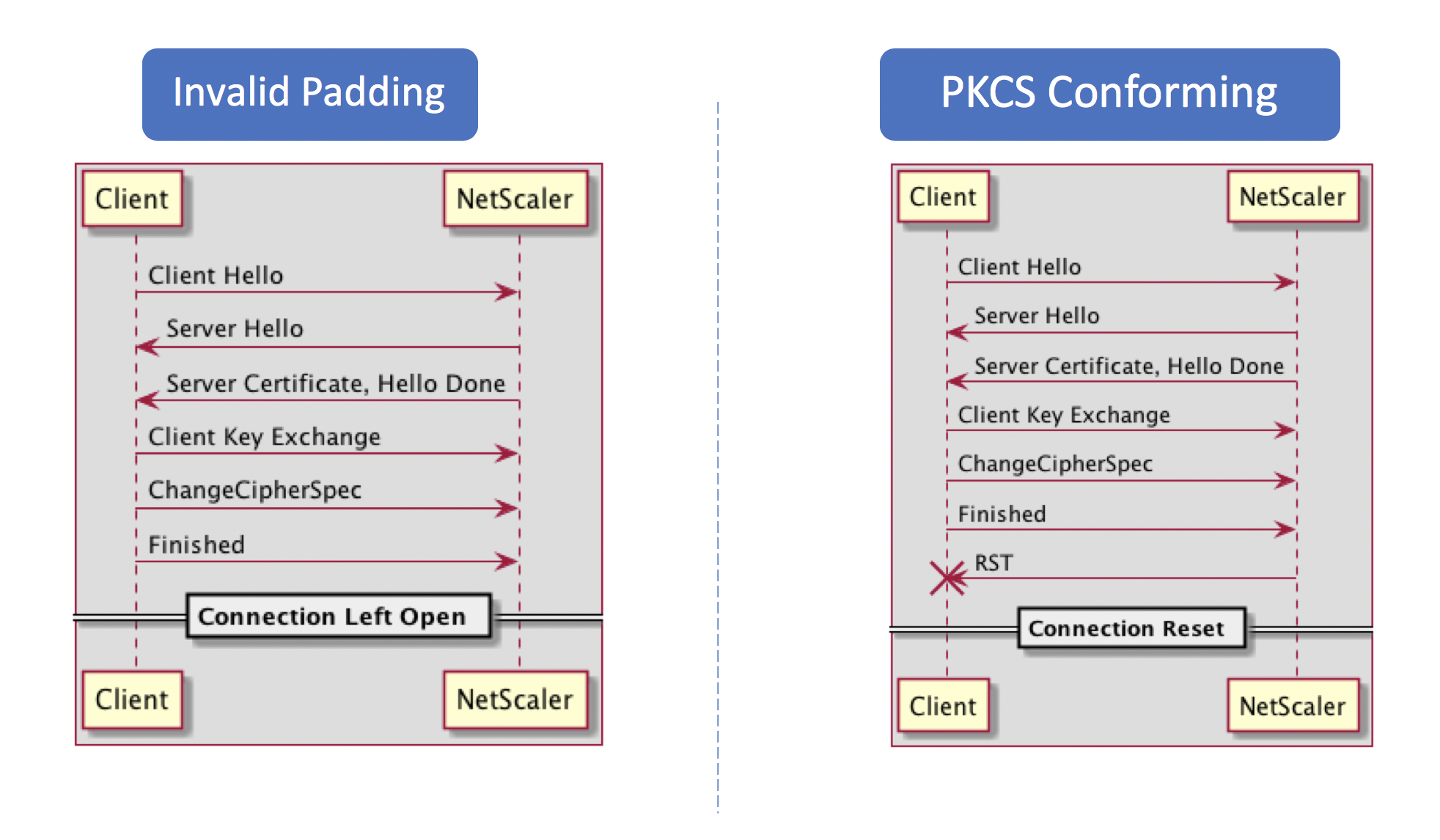
And Facebook was not alone...
F5 BigIP Oracle
Citrix NetScaler Oracle
Impact
If server or client only supports TLS_RSA modes then one can use Bleichenbacher attacks to directly decrypt traffic.
However RSA encryption modes aren't very popular any more, so this is often not the case.
If server and client support forward secrecy modes Man in the Middle attack may be possible, but requires performing attack very fast.
We have not tried this practically.
facebook.com wasn't the only vulnerable host
apple.com
cisco.com
ebay.com
paypal.com
accountservices.microsoft.com
Tracking down vendors is hard
Vendors / Products
F5, Citrix, Radware, Cisco ACE and ASA, Bouncy Castle, Erlang, WolfSSL, Palo Alto Networks, IBM, Symantec, Unisys, Cavium
Cisco ACE
Vulnerability is particularly severe, because these devices support no other cipher modes.
Cisco: We won't fix it, it's out of support for several years.
But there were plenty of webpages still running with these devices.
Like cisco.com
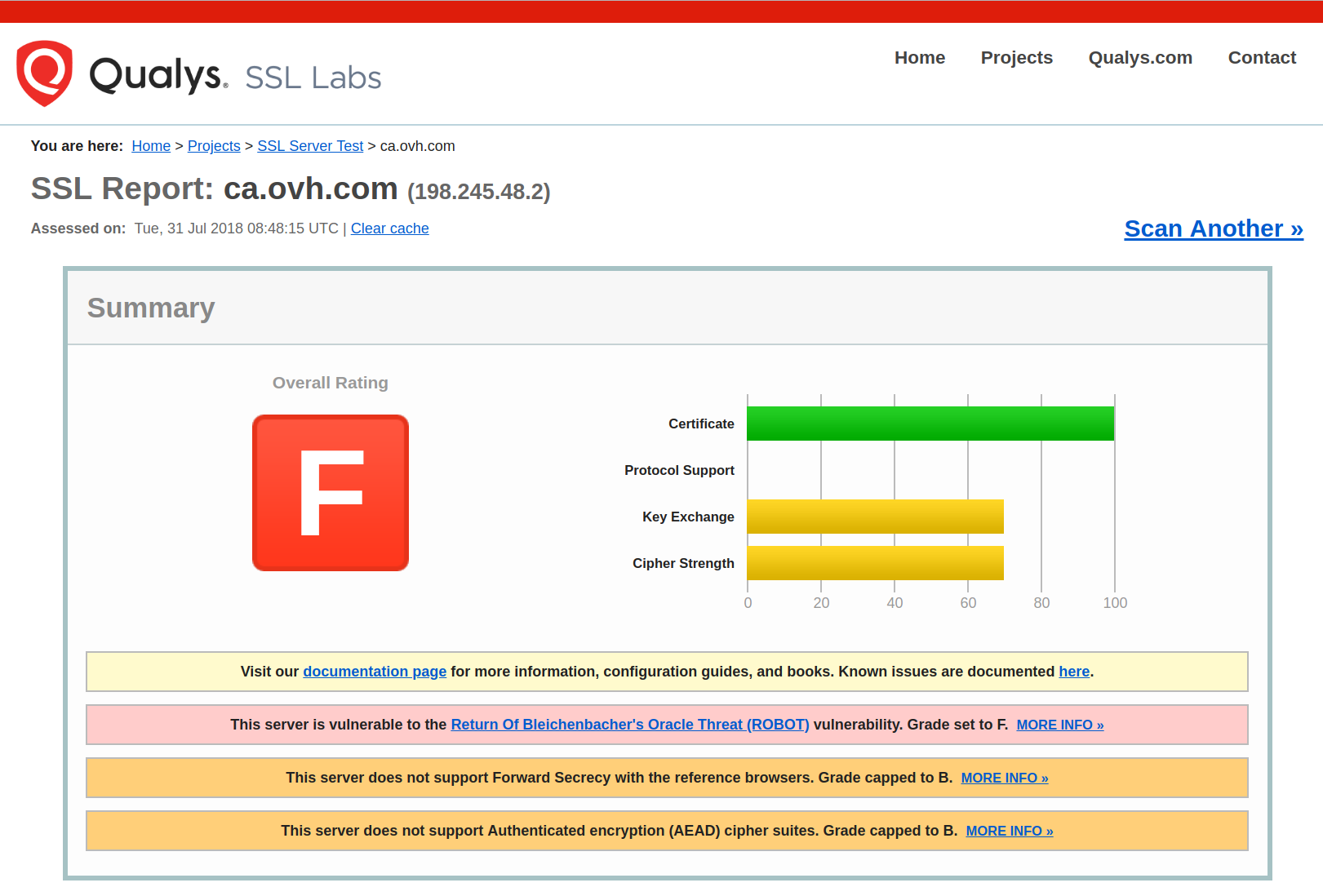
Apart from informing vendors and affected sites we also contacted developers of test tools (SSL Labs, testssl.sh, TLS Attacker, tlsfuzzer).
Before ROBOT no easily usable test tool for Bleichenbacher attacks was available.
CTF
- Decrypt message with vulnerable host.
- Find second host based on public key with Certificate Transparency
- Sign message with server key.
Timing
We did not consider timing based side-channels as part of this research.
It's known that some stacks don't implement the timing countermeasures (NSS has an open bug).
But even if you implement PKCS #1 1.5 according to the TLS 1.2 spec...
Crypto is math.
Cryptographic keys, signatures etc. are just large numbers.
Bignums
Cryptographic implementations use bignum libraries that allow numbers of arbitrary size.
Smaller numbers take less memory than larger numbers.
RSA
RSA decryption: M = C^d mod N
Result of this function with standard keysize (2048 bit) is 256 bytes large - usually.
RSA result
Or 255 bytes, or 254, depending on how many leading zeros the result has.
RSA bignum size sidechannel
Operating with smaller result leaves a small timing difference.
Practical?
We don't know.
This affects all major TLS libraries.
David Benjamin has fixed this in BoringSSL and submitted a pullrequest to OpenSSL.
Inconsistent Oracles
Some servers send certificates or "garbage bytes" in response to a bad ClientKeyExchange.
Communigate Pro is the only product we could identify with this behavior but there are others
Bleedinbacher anyone?
There could be a Heartbleed-style memory disclosure waiting to be found.
What to do?
If you run TLS disable TLS_RSA cipher suites.
TLS 1.3 no longer uses the RSA key exchange, but you're still at risk if you support older TLS versions and don't disable TLS_RSA.
Stop using RSA with PKCS #1 1.5!
If you want to use RSA use OAEP/PSS.
Takeaways
|
|