Cryptographic implementation flaws in TLS
Hanno Böck
https://hboeck.de/
Introduction
Hanno Böck
- Hacker and freelance Journalist
- Writes for Golem.de and others
- Author of Bulletproof TLS Newsletter
- Fuzzing Project (supported by the Core Infrastructure Initiative)
Every imaginable TLS implementation flaw can be found in the wild
Part 1:
Bleichenbacher's first Zombie
TLS crypto breakdown
- Web PKI / X.509 certificates (signatures)
- Handshake (asymmetric crypto)
- Data transmission (symmetric encryption and authentication)
Handshake
Client and Server want to get a Shared Secret
Two ways
- RSA Encryption
- Diffie Hellman (DHE or ECDHE) with Signatures (usually RSA)
Others
There are other ways (static DH, pre-shared key), but they're unused in mainstream protocols.
Forward Secrecy
Only Diffie Hellman variant provides Forward Secrecy.
After Snowden leaks and Heartbleed demand for Forward Secrecy grew considerably.
Let's look at RSA Encryption
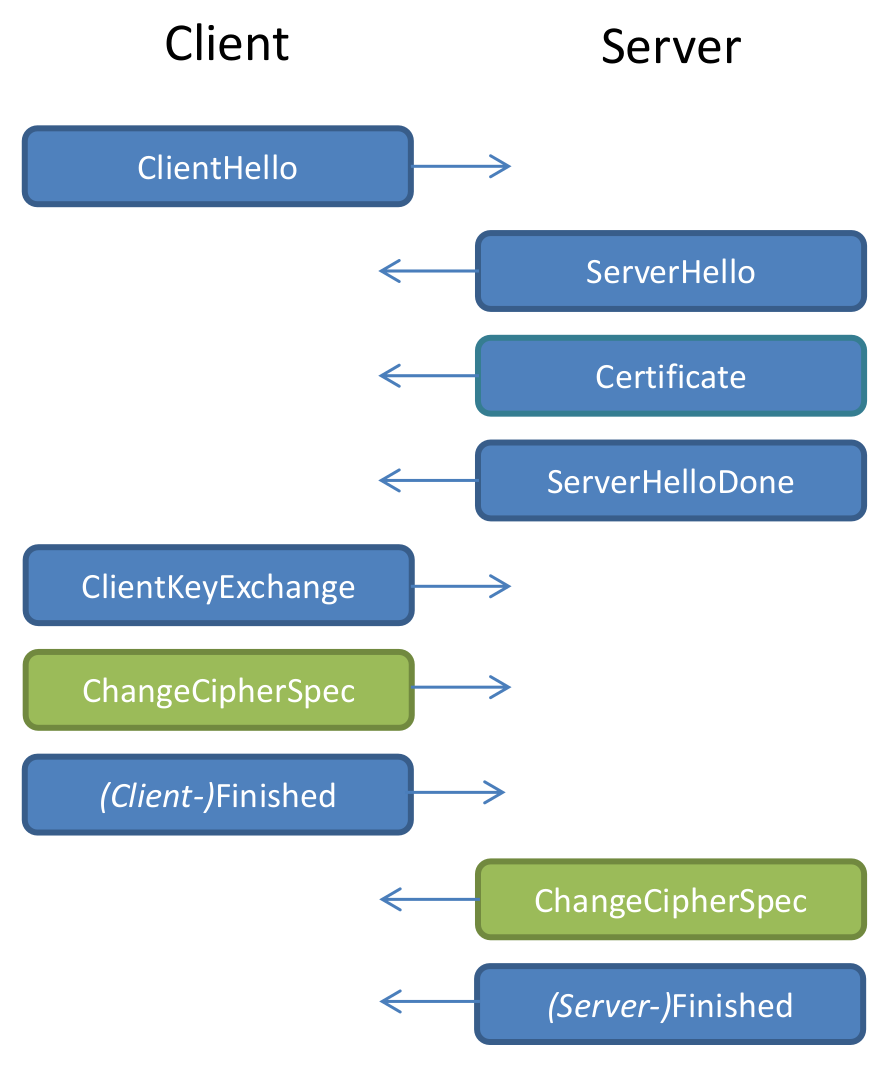
ClientKeyExchange
RSA-Encrypted Pre-Master Secret (random data)Naive RSA encryption
Message M · public key e, N · private key d
Encrypt: E = Me mod N
Decrypt: M = Ed mod N
It's wrong
Yet plenty of people teach it in crypto introductions. (Please stop!)
This naive variant is called Textbook RSA and totally insecure.
Why?
Encrypting the messages "0" and "1":
E = 0d mod N = 0
E = 1d mod N = 1
Padding
PKCS #1 1.5
Padding in TLS RSA Encryption
00 | 02 | [random] | 00 | 03 | 03 | [secret]
00 | 02 | [random] | 00 | 03 | 03 | [secret] ^^^^^^^
Block type (encryption)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes without zeros
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^
End of padding
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^
TLS Version from ClientHello
03 03 stands for TLS 1.2
(Don't ask, other story...)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes

Decrypted RSA block must always start with 00 02.
What should the server do if it doesn't?
Idea: Just reject the message with an error.
(e. g. "wrong block type prefix")
We just gave an attacker some information about encrypted data.
Correct prefix:
00 02 00 [...] 00 <= M < 00 03 00 [...] 00
Bad prefix:
M < 00 02 00 [...] 00 or M >= 00 03 00 [...] 00
RSA Malleability
2e * RSAEnc(M) = RSAEnc(2*M) 3e * RSAEnc(M) = RSAEnc(3*M) ne * RSAEnc(M) = RSAEnc(n*M)
Attacker can send ne*[encrypted block] to server and learn something about the range of n*[decrypted block].
Bleichenbacher developed an algorithm that allows fully decrypting an encrypted block based on an oracle that tells the attacker whether the block prefix is valid or not.
Variations
00 | 02 | [random] | 00 | 03 | 03 | [secret]
Depending on the checks done by the server (block prefix, padding length, TLS version) we get different oracles, gives more or less practical attacks.
How to fix?
Server must not give the client any information about the decrypted data.
The best way to avoid vulnerability to this attack is to treat incorrectly formatted messages in a manner indistinguishable from correctly formatted RSA blocks. Thus, when it receives an incorrectly formatted RSA block, a server should generate a random 48-byte value and proceed using it as the premaster secret. Thus, the server will act identically whether the received RSA block is correctly encoded or not.
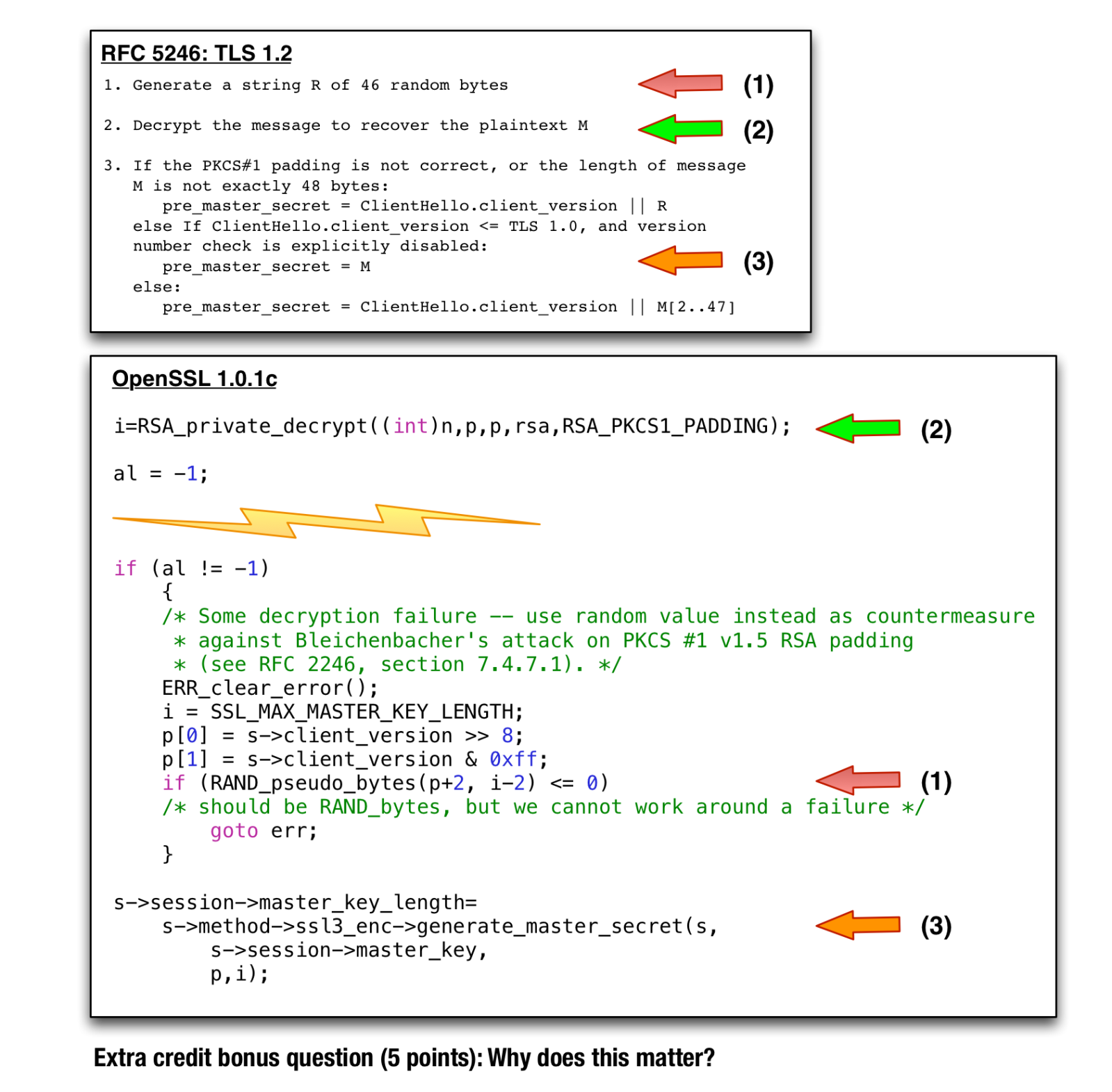
As described by Klima [KPR03], these vulnerabilities can be avoided
by treating incorrectly formatted message blocks and/or mismatched
version numbers in a manner indistinguishable from correctly
formatted RSA blocks. In other words:
1. Generate a string R of 46 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = ClientHello.client_version || R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
pre_master_secret = M
else:
pre_master_secret = ClientHello.client_version || M[2..47]
Note that explicitly constructing the pre_master_secret with the
ClientHello.client_version produces an invalid master_secret if the
client has sent the wrong version in the original pre_master_secret.
An alternative approach is to treat a version number mismatch as a
PKCS-1 formatting error and randomize the premaster secret
completely:
1. Generate a string R of 48 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
premaster secret = M
else If M[0..1] != ClientHello.client_version:
premaster secret = R
else:
premaster secret = M
Although no practical attacks against this construction are known,
Klima et al. [KPR03] describe some theoretical attacks, and therefore
the first construction described is RECOMMENDED.
In any case, a TLS server MUST NOT generate an alert if processing an RSA-encrypted premaster secret message fails, or the version number is not as expected. Instead, it MUST continue the handshake with a randomly generated premaster secret. It may be useful to log the real cause of failure for troubleshooting purposes; however, care must be taken to avoid leaking the information to an attacker (through, e.g., timing, log files, or other channels.)
Totally easy!
Of course everyone will get this right.
Or maybe not...

Bleichenbacher vulnerabilities have been found multiple times in many variations.
But everything is fixed now?
Maybe not...
Nobody has done any large scale checks, tools like SSL Labs don't test for those vulnerabilities.
--- openssl/crypto/rsa/rsa_pk1.c 2017-05-25 14:54:34.000000000 +0200
+++ openssl-broken/crypto/rsa/rsa_pk1.c 2017-10-02 14:57:25.766491083 +0200
@@ -156,8 +156,16 @@
p = (unsigned char *)to;
+ if ( getenv("BB98_TEST1") ) {
*(p++) = 0;
+ *(p++) = 17; /* Public Key BT (Block Type) */
+ } else if (getenv("BB98_TEST2")) {
+ *(p++) = 41;
*(p++) = 2; /* Public Key BT (Block Type) */
+ } else {
+ *(p++) = 0;
+ *(p++) = 2; /* Public Key BT (Block Type) */
+ }
/* pad out with non-zero random data */
j = tlen - 3 - flen;
@@ -170,12 +178,22 @@
if (RAND_bytes(p, 1) <= 0)
return (0);
} while (*p == '\0');
+ if ((i == 3) && (getenv("BB98_TEST3")))
+ *p = '\0';
p++;
}
*(p++) = '\0';
-
memcpy(p, from, (unsigned int)flen);
+
+ if (getenv("BB98_TEST0")) {
+ p[0] ^= 1;
+ p[1] ^= 41;
+ }
+ if (getenv("BB98_TEST4")) {
+ p[2] ^= 0xaa;
+ }
+
return (1);
}What would be a good fix?
TLS 1.3
Solution: Just stop supporting RSA Encryption, always do key exchanges with forward secrecy.
Sounds good?

Bleichenbacher's attack works cross-protocol.
Also cross-services (e. g. attacking HTTPS via vulnerable SMTP server).
This is also the reason why DROWN was an issue (Bleichenbacher attack on SSLv2).

RSA inverse property
RSA ecryption is equal to RSA signing.
If Bleichenbacher oracle allows decrypting RSA it also allows signing with server's private key.
No Key separation
Same keys are used for different protocol versions and for RSA signing and encryption.
As long as there is support for RSA key exchanges Bleichenbacher attacks remain a risk.
Backwards Compatibility!

TLS_RSA_WITH_AES_128_CBC_SHA
RSA Encryption is used in the compatibility cipher suite supported by most existing implementations and this is unlikely to change any time soon.
Why still support RSA Encryption?
- Mandatory to implement in TLS 1.2.
- Finite Field Diffie Hellman is getting deprecated for other reasons.
- Elliptic Curve Diffie Hellman deployment has been hindered by patent concerns.
Summary Bleichenbacher 98 attack
- It's one of the oldest attacks against SSL/TLS.
- It's been re-discovered in countless variations again and again.
- Plenty of implementations are vulnerable and nobody systematically checks for it.
- No proper fix is going to happen any time soon.