Part 4
Fuzzing Crypto

Bignum arithmetic

Crypto is math

Math is implemented in code and code has bugs

Security considerations for crypto usually simply assume the math is correct

Example

Modular Exponentiation

Modular Exponentiation

Basic operation widely used in public key cryptography.

(RSA, Diffie Hellman, ECC)

RSA-CRT

Optimization for RSA signatures using some precomputed values that are commonly part of the private key.

RSA-CRT intuition

Lenstra's attack on RSA-CRT

Given the input, the public key and a single signature where one of the calculations went wrong we can calculate the private key.

Lenstra, 1996

Math correctness

A single faulty modular exponentiation can leak the private key.

Powerful attack

• Exposing the private key.
• Any kind of error in the modular exponentiation works.

Does that really happen?

Of course!

Weimer, 2015

Guaranteeing 100% correctness of calculations is hard.

Not just software bugs, also hardware failures like Rowhammer.

To protect against this attack it's recommended to always verify signatures before exposing them.

Fuzzing

This may seem unrelated, but we'll get back to crypto soon.

Traditional Fuzzing

• Create (many) random inputs
• Feed inputs into software
• Wait until it crashes

Original:

{"name":"Smith","phone":[{"type":"home","no":"555-1234"}]}

Fuzzing:

{"nam":"Smith","phone":[{"type":"home","no":"555-1234"}]}
{"name�:"Smith","phone":[{"type":"home","no":"555-1234"}]}
{"oooooooooooooooooooooooonamee":"home","ns":555-1234"}]}
{"n����������ame":"Smith","phone"home","no":"555-1234"}]}
{"name":"Smith","phone":[{"typ�":"home"
{"name":"Smith","phone":[{"type"1111111111111111:-home","no":"555-123E"}]}
{"name":"Smith","pho�e":[{"ty`ee":[{"type":"home","no":
555":"home","no":
}]}

Dumb Fuzzing

Just perform random modifications on an input file.

Downsides

This will obviously only find shallow bugs.

Bugs triggered by rare inputs can't be found with dumb fuzzing (e.g. 1 out of 2¹²⁸ inputs).

Template-based Fuzzing

Create a fuzzer that "knows" something about its inputs.

Examples:

• Fill length fields with zero or maximum value.
• Create bogus combinations of features.
• Create syntactically correct, but bogus inputs.

Downsides

Lots of work.

This does not scale very well.

Modern (post-2014) Fuzzing

Coverage-guided Fuzzing

American Fuzzy Lop
(afl, afl-fuzz)

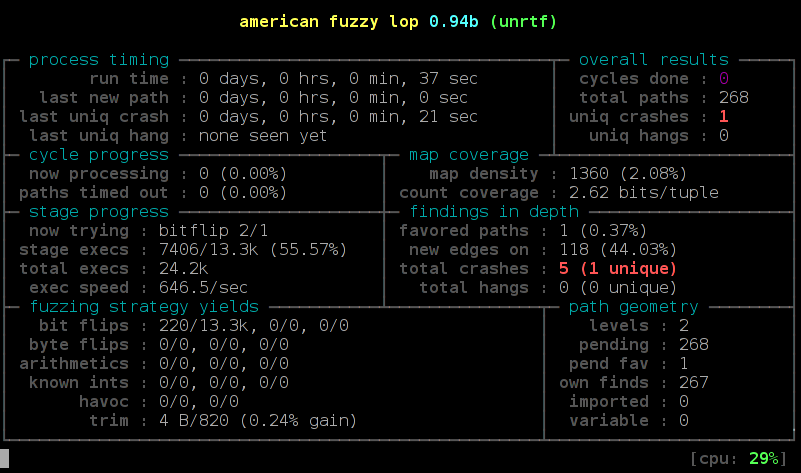
LibFuzzer

Like afl, but targets functions instead of executables.

In-process fuzzing, therefore much faster.

Back to bignum arithmetic

BN_sqr bug in OpenSSL
CVE-2014-3570

Security implications?

Can we find this bug with fuzzing?

Bug in 1 out of 1¹²⁸ inputs.

You can't hit this bug by chance.

Fuzzing BN_sqr

BN_sqr(r1, x);
BN_mul(r2, x, x, ctx);
assert(BN_cmp(r1, r2)==0);

Property-based Fuzz-Testing

"This will never work, but I should try it"
(Ralph-Philipp Weinmann at Black Hat 2015)

It actually works!

AFL is really good at finding bignum bugs

Differential Fuzz-Testing

Calculate same function with two different implementations, compare results.

AFL bignum trophies

• OpenSSL / BN_mod_exp (CVE-2015-3193)
• NSS / mp_div and mp_exptmod (CVE-2016-1938)
• Nettle / P-256 and P-385 scalar multiplications (CVE-2015-8803, CVE-2015-8804, CVE-2015-8805)
• OpenSSL / Poly1305
• MatrixSSL / pstm_exptmod (CVE-2016-6885, CVE-2016-6886, CVE-2016-6887)

MatrixSSL

Several of the devices with RSA-CRT bugs Florian Weimer discovered were using MatrixSSL.

The test input I reported to MatrixSSL had a modulus size unusual for crypto.

"Fix": MatrixSSL restricted the modulus size to common values (e. g. 2048).

So I had to find another input causing miscalculations with a 2048 bit modulus.

Why is fuzzing effective at finding bugs that can't be hit by chance?

Example inputs

BN_sqr, OpenSSL, CVE-2014-3570

E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E3 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E6 67 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 C7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7 E7

BN_mod_exp, OpenSSL, CVE-2015-0860

05 05 05 05 05 05² mod 41 41 41 41 41 41 41 41 41 41 41 27 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 80 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 05

mp_exptmod, NSS, CVE-2016-1938

80^FC mod 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0E ED 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 7C 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00

ecc_point_mul, Nettle, CVE-2015-8803

Point_P256(FF FF FF FF 00 00 00 01 00 00 00 00 00 00 00 00 00 00 00 00 FF FF FF FF FF FF FF FF 00 1C 2C 00, 97 31 27 5B 8E 97 3C EA FD 8A BF 5A 6E 16 A1 77 F0 5A 34 51 14 FB C7 52 7B 3A 60 BC 65 FE 60 6A) · 1

Repetitions!

Github

LLVM SVN

It really works

Later Google's oss-fuzz project found another bug in BN_mod_exp in Openssl with LibFuzzer (CVE-2017-3732).

Retroactive testing

Take known math implementation bug and try to find it with fuzzing.

This usually works.

Examples

• GCM bug in OpenSSL preview (The fragility of AES-GCM authentication algorithm, Gueron, Krasnov, 2013)
• Tweetnacl Carrybit bug

These can be found with LibFuzzer in seconds.

Open question: Are there such bugs where Fuzzing fails?

Formal Verification

A discussion about Fuzzing versus Formal Verification

Formal verification

I have to admit something: I don't know a whole lot about formal verification.

Formal verification

These things are hardly controversial:

• Formal verification is a lot of work.
• It's hard to apply it to real world software.
• It often comes with limitations and caveats.
• Most cryptographic algorithm implementations are not formally verified.

Beringer et al, 2015

This is disingenuous

Mozilla works on formally verified Crypto

Taubert, 2017

Zinzindohoué et al, 2017

Conclusion

• Differential Fuzz-Testing is extremely effective at finding bugs in basic math and crypto functions.
• There are open questions about the how and why.
• Formal Verification may be interesting for the future, but it's no replacement for other bug finding techniques any time soon.