ROBOT
Return of Bleichenbacher's Oracle Threat
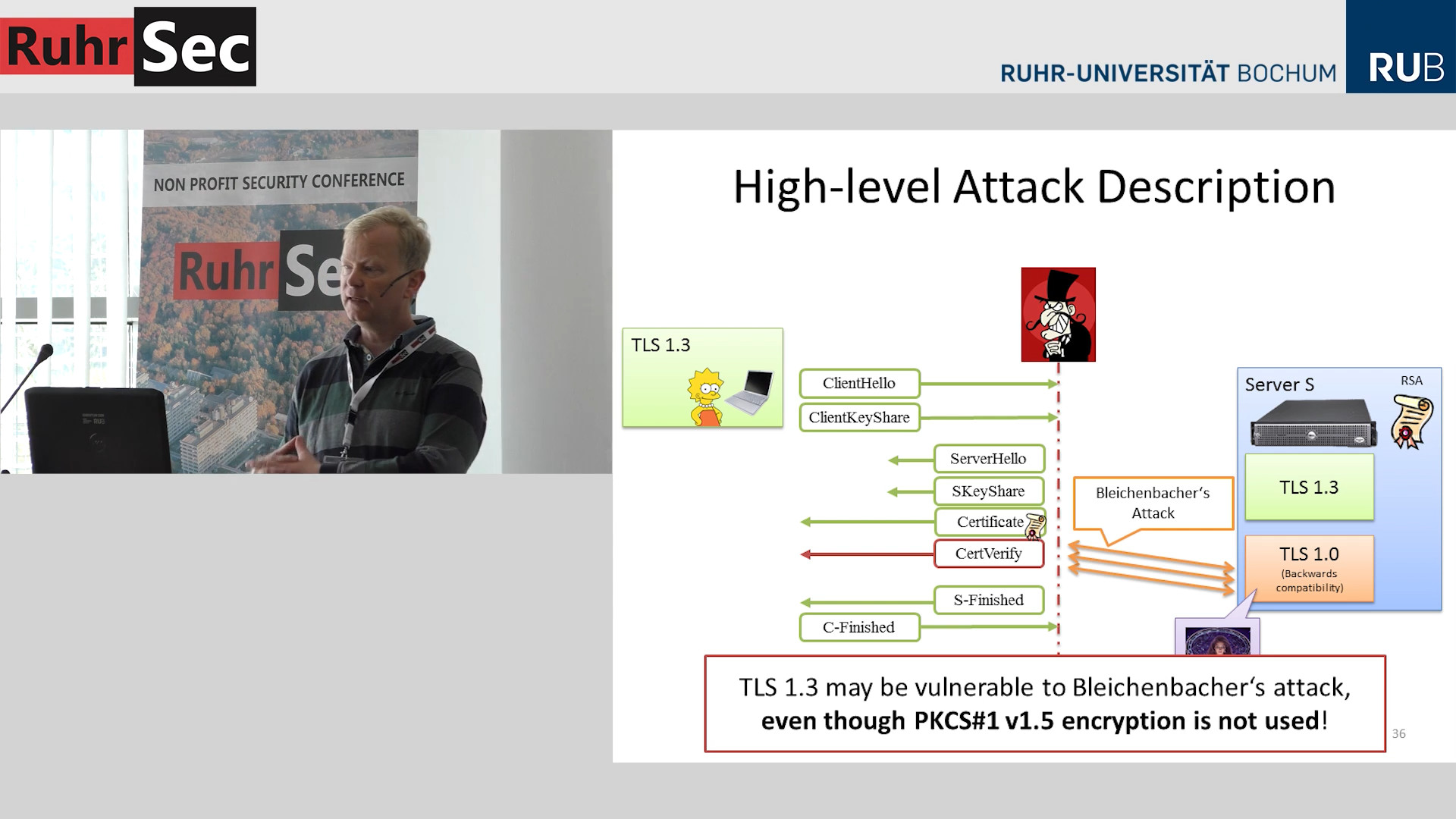
RuhrSec 2016: "Transport Layer Security – TLS 1.3 and backwards security issues", Jörg Schwenk
If your TLS RSA encryption is vulnerable to Bleichenbacher attacks then this might be a problem even for TLS 1.3, which does not support RSA encryption.
How's that possible? Cross-protocol attacks.
But what are these Bleichenbacher attacks? And are there any vulnerable implementations?

Let's look at the TLS handshake
Client and Server want to get a Shared Secret
Two ways
- RSA Encryption
- Diffie Hellman (DHE or ECDHE) with Signatures (usually RSA), provides forward secrecy
Let's look at RSA Encryption
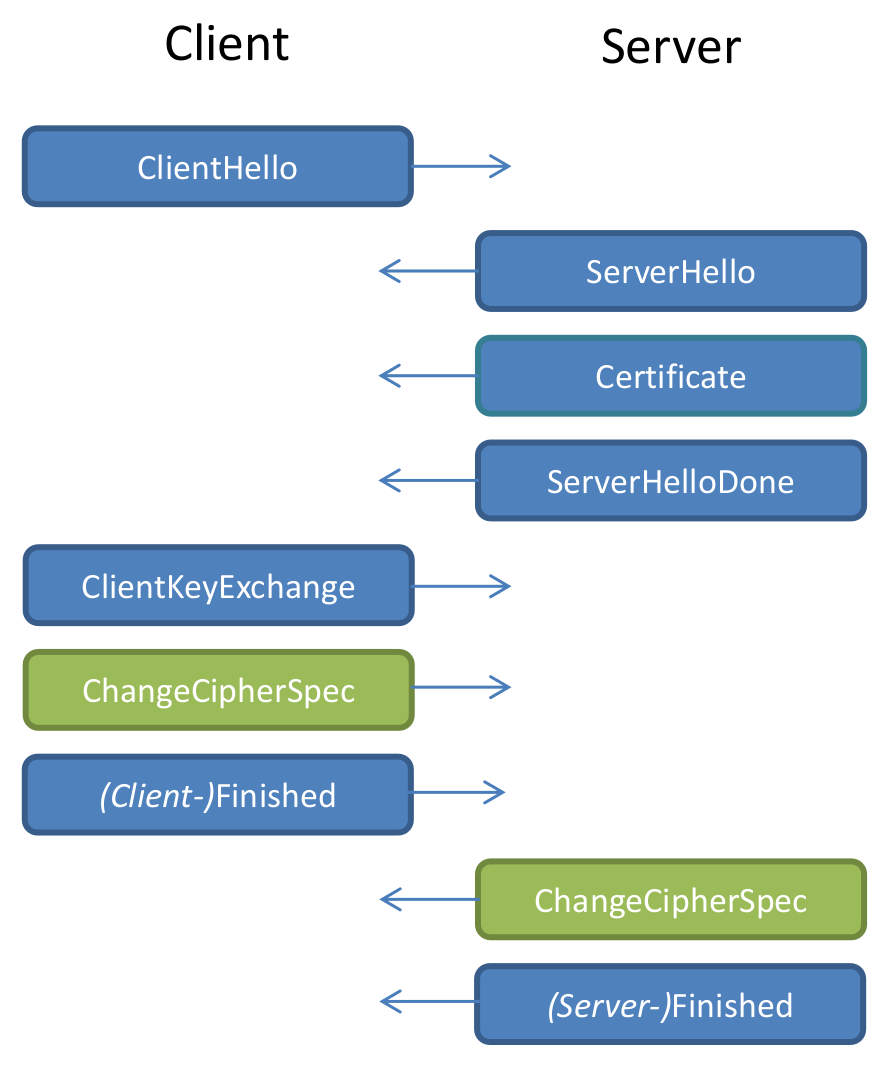
ClientKeyExchange
RSA-Encrypted Pre-Master Secret (random data)Naive RSA encryption
Message M · public key e, N · private key d
Encrypt: E = Me mod N
Decrypt: M = Ed mod N
This naive variant is called Textbook RSA and totally insecure.
Why?
Encrypting the messages "0" and "1":
E = 0d mod N = 0
E = 1d mod N = 1
Padding
PKCS #1 1.5
Padding in TLS RSA Encryption
00 | 02 | [random] | 00 | 03 | 03 | [secret]
00 | 02 | [random] | 00 | 03 | 03 | [secret] ^^^^^^^
Block type (encryption)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes without zeros
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^
End of padding
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^
TLS Version from ClientHello
03 03 stands for TLS 1.2
(Don't ask, other story...)
00 | 02 | [random] | 00 | 03 | 03 | [secret]
^^^^^^^^
Random bytes
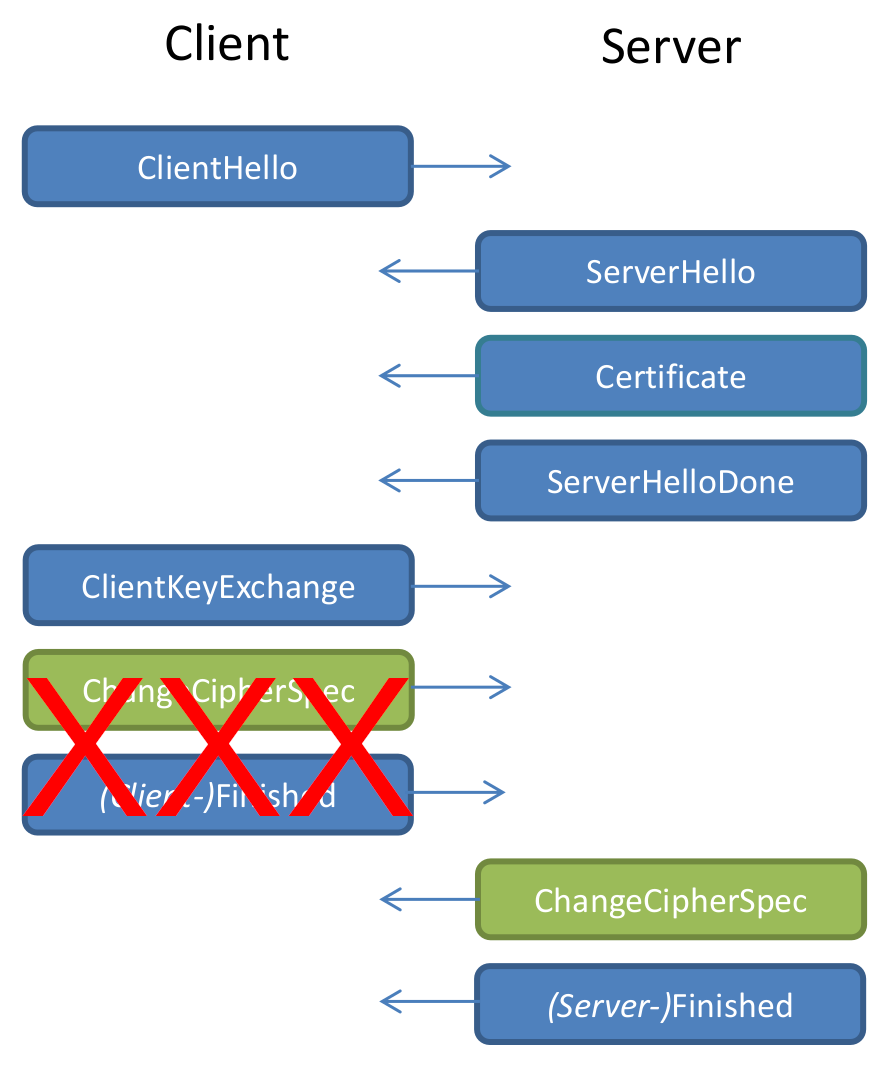
Decrypted RSA block must always start with 00 02.
What should the server do if it doesn't?
Idea: Just reject the message with an error.
(e. g. "wrong block type prefix")
We just gave an attacker some information about encrypted data.
Correct prefix:
00 02 00 [...] 00 <= M < 00 03 00 [...] 00
Bad prefix:
M < 00 02 00 [...] 00 or M >= 00 03 00 [...] 00
RSA Malleability
2e * RSAEnc(M) = RSAEnc(2*M) 3e * RSAEnc(M) = RSAEnc(3*M) ne * RSAEnc(M) = RSAEnc(n*M)
Attacker can send ne*[encrypted block] to server and learn something about the range of n*[decrypted block].
Bleichenbacher developed an algorithm that allows fully decrypting an encrypted block based on an oracle that tells the attacker whether the block prefix is valid or not.
Variations
00 | 02 | [random] | 00 | 03 | 03 | [secret]
Depending on the checks done by the server (block prefix, padding length, TLS version) we get different oracles, gives more or less practical attacks.
Impact
If server or client only supports TLS_RSA modes then one can use Bleichenbacher attacks to directly decrypt traffic.
If server and client support forward secrecy modes Man in the Middle attack may be possible, but requires performing attack very fast.
How to fix?
Server must not give the client any information about the decrypted data.
The best way to avoid vulnerability to this attack is to treat incorrectly formatted messages in a manner indistinguishable from correctly formatted RSA blocks. Thus, when it receives an incorrectly formatted RSA block, a server should generate a random 48-byte value and proceed using it as the premaster secret. Thus, the server will act identically whether the received RSA block is correctly encoded or not.
As described by Klima [KPR03], these vulnerabilities can be avoided
by treating incorrectly formatted message blocks and/or mismatched
version numbers in a manner indistinguishable from correctly
formatted RSA blocks. In other words:
1. Generate a string R of 46 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = ClientHello.client_version || R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
pre_master_secret = M
else:
pre_master_secret = ClientHello.client_version || M[2..47]
Note that explicitly constructing the pre_master_secret with the
ClientHello.client_version produces an invalid master_secret if the
client has sent the wrong version in the original pre_master_secret.
An alternative approach is to treat a version number mismatch as a
PKCS-1 formatting error and randomize the premaster secret
completely:
1. Generate a string R of 48 random bytes
2. Decrypt the message to recover the plaintext M
3. If the PKCS#1 padding is not correct, or the length of message
M is not exactly 48 bytes:
pre_master_secret = R
else If ClientHello.client_version <= TLS 1.0, and version
number check is explicitly disabled:
premaster secret = M
else If M[0..1] != ClientHello.client_version:
premaster secret = R
else:
premaster secret = M
Although no practical attacks against this construction are known,
Klima et al. [KPR03] describe some theoretical attacks, and therefore
the first construction described is RECOMMENDED.
In any case, a TLS server MUST NOT generate an alert if processing an RSA-encrypted premaster secret message fails, or the version number is not as expected. Instead, it MUST continue the handshake with a randomly generated premaster secret. It may be useful to log the real cause of failure for troubleshooting purposes; however, care must be taken to avoid leaking the information to an attacker (through, e.g., timing, log files, or other channels.)
Totally easy!
Of course everyone will get this right.
Or maybe not...
Let's test
Send different broken RSA-encrypted ClientKeyExchange packages.
If replies differ we have an oracle.
TLS alerts, Duplicat TLS alerts, TCP connection resets, Timeouts
First hit: facebook.com
We have to attack Facebook!
After several tries we did it! We successfully signed a message with Facebook's private key.
We reported it to Facebook. They fixed it.
Then we figured out a way to attack the same servers again.
But facebook wasn't alone.
apple.com
cisco.com
ebay.com
paypal.com
accountservices.microsoft.com
web.de
Tracking down vendors is hard
Vendors / Products
F5, Citrix, Radware, Cisco ACE and ASA, Bouncy Castle, Erlang, WolfSSL, Palo Alto Networks, IBM
Cisco ACE
Vulnerability is particularly severe, because these devices support no other cipher modes.
Cisco: We won't fix it, it's out of support for several years.
But there were plenty of webpages still running with these devices.
Like cisco.com
Apart from informing vendors and affected sites we also contacted developers of test tools (SSL Labs, testssl.sh, TLS Attacker, tlsfuzzer).
Before ROBOT no easily usable test tool for Bleichenbacher attacks was available.
CTF
- Decrypt message with vulnerable host.
- Find second host based on public key with Certificate Transparency
- Sign message with server key.
Timing
We did not consider timing based side-channels as part of this research.
It's known that some stacks don't implement the timing countermeasures (NSS has an open bug).
But even if you implement PKCS #1 1.5 according to the TLS 1.2 spec...
Crypto is math.
Cryptographic keys, signatures etc. are just large numbers.
Bignums
Cryptographic implementations use bignum libraries that allow numbers of arbitrary size.
Smaller numbers take less memory than larger numbers.
RSA
RSA decryption: M = C^d mod N
Result of this function with standard keysize (2048 bit) is 256 bytes large - usually.
RSA result
Or 255 bytes, or 254, depending on how many leading zeros the result has.
RSA bignum size sidechannel
Operating with smaller result leaves a small timing difference.
Practical?
I don't know.
This affects all major TLS libraries.
It's probably worth investigating and writing a paper about it.
Conclusion
Stop using PKCS #1 1.5
The most surprising thing about ROBOT is how straightforward this was.
Take an existing, very well known TLS vulnerability and scan for it.
Do some minor modifications to find more.
Nothing what we did was sophisticated or required advanced crypto knowledge.